用于推荐系统的知识图卷积网络

科研 Knowledge Graph 论文翻译 Recommendation
科研
发布日期:   2021-04-01
文章字数:   8.3k

用于推荐系统的知识图卷积网络

论文信息

arXiv:1904.12575v1 [cs.IR] 18 Mar 2019

WWW ‘19: The Web Conference San Francisco CA USA May, 2019, pp. 3307-3313, 2019.

2019年WWW会议，国际万维网会议，A类交叉会议

摘要

为了==减轻基于协作过滤的稀疏和冷启动问题==，研究人员和工程师通常收集==用户和项目的属性==，并设计精细算法以利用这些附加信息。通常，该属性不是相互隔绝的而是彼此连接的，这可以从知识图（KG）中得到。

在本文中，我们提出了==知识图形卷积网络（KGCN）==，一个端到端框架，通过在KG上挖掘它们的关联属性有效地捕获项目间的相关性。

为了自动发现KG的==高阶结构信息和语义信息==，我们对KG中每个实体的邻居进行取样得到其表示，然后使用偏重bias结合邻近信息来进行计算一个给定实体的表示。

可以将接收领域扩展到距离频率的多个跳跃，以模拟高阶邻近信息并捕获用户的潜在的长距离兴趣。

此外，我们以小批次方式实现提出的KGCN，这使我们的模型能够在大型数据集和KG上运行。

我们将拟议的模型应用于关于电影，书籍和音乐推荐的三个数据集，实验结果表明我们的方法优于强大的推荐基线。

关键词

  • 推荐系统
  • 知识图谱
  • 图卷积网络

1. 简介

推荐问题

随着互联网技术的推进，人们可以访问大量的在线内容，如新闻[25]，电影[5]和商品[26]。

在线平台的一个臭名昭着的问题是，物品的数量可以压倒用户。为了减轻信息过多的影响，可以用推荐系统（RS）来搜索并推荐一小部分物品以满足用户的个性化兴趣。

传统推荐技术是协作滤波（CF），其分配用户和项目的基于ID的表示向量，然后通过特定操作（如内部产品[16]或神经网络）进行模拟它们的交互[8]。

然而，==基于CF的方法通常遭受用户项目交互的稀疏性和冷启动问题==。为了解决这些限制，研究人员通常转向具有丰富的功能，其中==用户和物品的属性==用于补偿稀疏性并提高建议的性能[3,17]。

知识图谱用于推荐

最近的一些研究[9,18,19,22-24]比简单地使用属性进一步走了一步：

它们指出了该==属性不是被隔绝的，而是彼此联系，这形成了知识图（kg）==。

通常，kg是指向的异构图，其中节点对应于实体（项目或项目属性）和边缘对应于关系。

与无功的方法相比，==将KG纳入推荐中的提议==，其中三种方式有利于结果[18]：

  1. KG项目中的丰富语义相关性可以帮助探索其潜在的连接并提高结果的精度;
  2. KG各种关系对于合理地扩展用户的兴趣以及增加推荐物品的多样性有助于扩展用户的兴趣;
  3. kg连接用户的历史上最受欢迎和推荐的项目，从而为推荐系统带来可解释性。

尽管有上述好处，但由于其高维度和异质性，利用KG在RS中是相当挑战。

知识图片嵌入方法

一种可行的方式是通过==知识图形嵌入（KGE）方法[20]预处理KG==，将其映射实体和与低维表示向量的关系[9,19,23]。

然而，普通使用的KGE方法侧重于建模严格的语义相关性（例如，Transe [1]和Transr [12]假设头+关系=尾部），其更适合于图形应用程序，例如KG完成和链接预测比推荐。

知识图谱结构图形算法

一种更自然和直观的方式是==利用KG结构直接设计图形算法==。

1.FMG

例如，每个[22]和FMG [24]将kg作为异构信息网络，并提取基于元路径/元图的潜在特征，以表示用户和项目之间的连接沿不同类型的关系路径/图形。

然而，每次和FMG严重依赖于手动设计的元路径或元图，这几乎不会在现实中最佳。

2.RippleNet

Ripplenet [18]是一种类似的内存网络型模型，可在KG中传播用户的潜在偏好，并探讨其分层兴趣。但注意，关系的重要性在突破平板上略微表征，因为关系R的嵌入矩阵几乎不能接受训练，以捕获二次形式的$V^⊤Rh$（v和h是两个实体的嵌入矢量）的重要特征。另外，Ripple集合的大小可以随着KG大小的增加而不可预测的，这引起了巨大的计算和存储开销。

本文提出KGCN

在本文中，我们调查了KG结合推荐的问题。

我们的设计目标是在KG中自动捕获高阶结构和语义信息。

灵感来自图卷积网络（GCN）1，尝试将卷积概括为图形域，我们向推荐系统提出知识图形卷积网络（KGCN）。

当计算KG中给定实体的表示时，==KGCN的关键概念是聚合和合并邻居信息==。

这种设计具有两个优点：

（1）通过邻域聚合的操作，成功捕获本地接近结构并将其存储在每个实体中。

（2）邻居被依赖于连接关系和特定用户的分数加权，其特征在于KG和用户的个性化兴趣的语义信息。

请注意，在最坏情况下，一个实体的邻居size可能会非常非常的大。因此，我们将==每个节点的固定尺寸邻域==作为接收领域进行采样，这使得kgcn的成本可预测。

给定实体的邻域定义也可以分层扩展到多跳（多个跳跃？就是多走几次节点？）之外，以建模高阶实体依赖关系并捕捉用户的潜在远程兴趣。

数据集及结果

根据实验，我们将KGCN应用于三个数据集:MovieLens-20M(电影)、Book-Crossing (书籍)和Last.FM(音乐)。
实验结果表明，与最先进的推荐基准相比，KGCN在电影、书籍和音乐推荐中的平均AUC增益分别为4.4%、8.1%和6.2%。

本文贡献

我们在本文中的贡献总结如下:

  • 我们提出了知识图卷积网络，这是一个端到端的框架，用于为推荐系统探索用户对知识图的偏好。通过扩展KG中每个实体的接受域，KGCN能够捕捉用户的高阶个性化兴趣。
  • 我们在三个真实世界的推荐场景中进行实验。结果证明了KGCN最小二乘法在最先进的基线上的有效性。
  • 我们向研究人员发布KGCN代码和数据集(知识图)，以验证报告的结果并进行进一步的研究。代码和数据可在https://github.com/hwwang55/KGCN获得 (本地文件夹在这)

2. 相关工作

本文方法

我们的方法在概念上受到GCN（图卷积网络）的启发。

一般来说，GCN可以分为==光谱方法和非光谱方法==。

谱方法表示图形，并在谱空间中执行卷积。

例如，布鲁纳等人[2]定义了傅立叶域中的卷积，并计算了图拉普拉斯的特征分解，

德费拉德等人[4]通过图拉普拉斯的切比雪夫展开来近似卷积滤波器，

Kipf等人[10]通过谱图卷积的局部一阶近似提出了卷积结构。

相比之下，非谱方法直接对原始图进行操作，并为节点组定义卷积。

为了处理不同大小的邻域并保持CNN的权重共享特性，研究人员建议为每个节点度学习一个权重矩阵[6]，从图中提取局部连通区域[13]，或者采样一组固定大小的邻域作为支持大小[7]。

我们的工作可以看作是一种==特殊类型图(即知识图)的非谱方法==。

我们的方法也连接到PinSage [21]和GAT [15]。

但是请注意，PinSage和GAT都是为同构图设计的。

我们的工作与文献的主要区别在于，我们借助==异构知识图==为推荐系统提供了一个新的视角。

相关知识：关于图卷积网络

GCN的概念首次提出于ICLR2017（成文于2016年）

简介

回忆一下，我们做图像识别，对象是图片，是一个二维的结构，于是人们发明了CNN这种神奇的模型来提取图片的特征。
CNN的核心在于它的kernel，kernel是一个个小窗口，在图片上平移，通过卷积的方式来提取特征。
这里的关键在于图片结构上的平移不变性：一个小窗口无论移动到图片的哪一个位置，其内部的结构都是一模一样的，因此CNN可以实现参数共享。
这就是CNN的精髓所在。

再回忆一下RNN系列，它的对象是自然语言这样的序列信息，是一个一维的结构，RNN就是专门针对这些序列的结构而设计的，通过各种门的操作，使得序列前后的信息互相影响，从而很好地捕捉序列的特征。

图（这里应该是数据结构图Graph）的结构一般来说是十分不规则的，可以认为是无限维的一种数据，所以它没有平移不变性。
每一个节点的周围结构可能都是独一无二的，这种结构的数据，就让传统的CNN、RNN瞬间失效。所以很多学者从上个世纪就开始研究怎么处理这类数据了。这里涌现出了很多方法，例如GNN、DeepWalk、node2vec等等，GCN只是其中一种，这里只讲GCN，其他的后面有空再讨论。

==GCN，图卷积神经网络，实际上跟CNN的作用一样，就是一个特征提取器，只不过它的对象是图数据==。
GCN精妙地设计了一种从图数据中提取特征的方法，从而让我们可以使用这些特征去对图数据进行
==节点分类（node classification）、图分类（graph classification）、边预测（link prediction），还可以顺便得到图的嵌入表示（graph embedding）==，可见用途广泛。
因此现在人们脑洞大开，让GCN到各个领域中发光发热。

数学表示

假设我们手头有一批图数据，其中有N个节点（node），每个节点都有自己的特征，我们设这些节点的特征组成一个N×D维的矩阵X，然后各个节点之间的关系也会形成一个N×N维的矩阵A，也称为邻接矩阵（adjacency matrix）。X和A便是我们模型的输入。

  • N个节点
  • 节点特征矩阵：$N \times D$ 维矩阵 X
  • 节点关系矩阵：$N \times N$ 维矩阵A，邻接矩阵
  • 输入：节点特征矩阵X，节点关系矩阵A

GCN也是一个神经网络层，它的层与层之间的传播方式是：

img

这个公式中：

  • $\tilde A = A + I$，I是单位矩阵
  • $\tilde D$是$\tilde A$的度矩阵（degree matrix），公式为
  • H是每一层的特征，对于输入层的话，H就是X
  • σ是非线性激活函数

我们先不用考虑为什么要这样去设计一个公式。我们现在只用知道：

这个部分，是可以事先算好的，因为D波浪由A计算而来，而A是我们的输入之一。==A输入可以计算得到D，在第一层时H就是X，σ 是给出的激活函数，W是参数矩阵==

所以对于不需要去了解数学原理、只想应用GCN来解决实际问题的人来说，你只用知道：哦，这个GCN设计了一个牛逼的公式，用这个公式就可以很好地提取图的特征。这就够了，毕竟不是什么事情都需要知道内部原理，这是根据需求决定的。

直观例子

img

上图中的GCN输入一个图，通过若干层GCN每个node的特征从X变成了Z，但是，无论中间有多少层，node之间的连接关系，即A，都是共享的。

假设我们构造一个两层的GCN，激活函数分别采用ReLU和Softmax，则整体的正向传播的公式为：

img

最后，我们针对所有带标签的节点计算cross entropy损失函数：

img

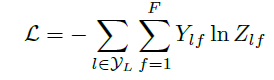
就可以训练一个node classification的模型了。由于即使只有很少的node有标签也能训练，作者称他们的方法为==半监督分类==。

当然，==你也可以用这个方法去做graph classification、link prediction，只是把损失函数给变化一下即可==。

公式中的与对称归一化拉普拉斯矩阵十分类似，而在谱图卷积的核心就是使用对称归一化拉普拉斯矩阵，这也是GCN的卷积叫法的来历。

GCN 有多牛

在看了上面的公式以及训练方法之后，我并没有觉得GCN有多么特别，无非就是一个设计巧妙的公式嘛，也许我不用这么复杂的公式，多加一点训练数据或者把模型做深，也可能达到媲美的效果呢。

但是一直到我读到了论文的附录部分，我才顿时发现：GCN原来这么牛啊！

为啥呢？

因为即使不训练，==完全使用随机初始化的参数W==，GCN提取出来的特征就以及十分优秀了！这跟CNN不训练是完全不一样的，后者不训练是根本得不到什么有效特征的。

还没训练就已经效果这么好，那给==少量的标注信息==，GCN的效果就会更加出色。

  1. 对于很多网络，我们可能==没有节点的特征==，这个时候可以使用GCN吗？答案是可以的，如论文中作者对那个俱乐部网络，采用的方法就是用单位矩阵 I 替换特征矩阵 X。
  2. 我==没有任何的节点类别的标注==，或者什么其他的标注信息，可以使用GCN吗？当然，就如前面讲的，不训练的GCN，也可以用来提取graph embedding，而且效果还不错。
  3. GCN网络的层数多少比较好？论文的作者做过GCN网络深度的对比研究，在他们的实验中发现，==GCN层数不宜多，2-3层的效果就很好了==。

3. 知识图卷积网络

在这一节中，我们介绍提出的KGCN模型。

  1. 我们首先提出了知识图感知推荐问题。
  2. 然后我们展示了单层KGCN的设计。
  3. 最后，我们介绍了完整的KGCN学习算法，以及它的具体实现。

3.1 问题提出

我们将知识图感知推荐问题公式化如下。

在一个典型的推荐场景中，我们有一组==M个用户==U = {u1，u2，…，uM}和一组==N项==V = {v1，v2，…，vN}。

根据用户的==隐反馈==定义的==用户-项目交互矩阵==Y ∈ RM×Nis，其中yuv= 1表示用户u参与项目v，如点击、浏览或购买；otherwiseyuv= 0。

此外，我们还有一个==知识图G==，它由实体-关系-实体三元组(h，r，t)组成。这里h ∈ E，r ∈ R，t ∈ E表示知识三元组的头，关系，尾，E和R分别是知识图中实体和关系的集合。

例如，三部曲(冰与火之歌，书.书.作者，乔治·马丁)陈述了乔治·马丁写《冰与火之歌》这本书的事实。

在很多推荐场景中，一个item v ∈ V对应一个实体e ∈ E，比如在书籍推荐中，“冰与火之歌”这一项也作为同名实体出现在知识图中。

  • 用户user，物品item
  • 隐反馈矩阵Y，1是交互，0是无交互
  • 知识图G，其中的三元组(h,r,t)
  • 一个item就对应一个知识图G中的实体e

给定用户-项目交互矩阵Y和知识图G，我们旨在预测用户u是否对他以前没有交互过的项目有潜在兴趣。

我们的目标是学习一个预测函数$\hat y _{uv} = \mathcal F(u,v | \Theta,Y,G) $，其中$\hat y _{uv}$表示用户u将参与项目v的概率，θ表示函数F的模型参数。

  • 输入：隐反馈矩阵Y，知识图G
  • 目标：$\hat y _{uv} = \mathcal F(u,v | \Theta,Y,G) $
    • $\hat y _{uv}$表示用户 u 将参与项目 v 的==概率==
    • θ表示函数F的==模型参数==

3.2 KGCN层

KGCN被用来在知识图中捕捉实体之间的高阶结构邻近性。

在这一小节中，我们首先描述==单个KGCN层==。

考虑用户u和项目(实体)v的候选对。

我们用N (v)来表示直接连接到实体v的其他实体集合，和$r_{e_i,e_j}$来表示 实体$e_i$和$e_j$之间的关系。

  • 用户u，实体v
  • N(v)：实体v的邻居实体集合
  • $r_{e_i,e_j}$ ：实体$e_i$和$e_j$之间的关系

我们还使用函数$\mathcal g : \mathbb R^d \times \mathbb R ^d \rightarrow \mathbb R$​ (例如内积)来计算==用户和关系之间的分数==：

image-20210402172958608

其中$u ∈ \mathbb R^d$和$r ∈ \mathbb R^d$分别表示用户u和关系R，d是表示的维数。一般来说，$\pi _r ^u$表征关系对用户的重要性。

例如，一个用户可能对与他历史上喜欢的电影共享同一“明星”的电影有更多的潜在兴趣，而另一个用户可能更关心电影的“流派”。

  • $\pi _r ^u$：代表关系对于用户的重要性（比如“actor_is”、“type_is”）关系
  • u：用户，$u ∈ \mathbb R^d$，d维数
  • r：关系，$r ∈ \mathbb R^d$，d维数

为了==刻画物品v的拓扑邻近结构==，我们计算了==v的邻域的线性组合==:

image-20210402201234277

其中，$\tilde \pi {r{v,e}} ^u$是==标准化的用户关系得分==：

image-20210402201405937

当计算一个实体的邻域表示时，用户-关系分数充当个性化过滤器，因为我们聚集带有偏差的邻居来代表那些特定用户的分数。

  • e为实体v的邻域中的实体；
  • r是实体v与邻居e的关系

在现实世界的知识图中，N (e)的大小在所有实体中可能有很大的不同。

为了保持每批的计算模式固定和更高效，我们为==每个实体统一采样一组固定大小的邻居==，而不是使用它的全部邻居。

具体来说，我们将==实体的邻域==表示计算为$v^u _{S(v)}$ ，其中$S(v) = {e | e \sim N(v)}$ 且$|S(v)| = K $ 是一个可配置的常量。

在KGCN，S(v)也被称为实体v的(单层)感受野，因为v的最终表征对这些位置很敏感。

图1a给出了给定实体的两层感受野的说明性例子，其中K被设置为2。

image-20210402204045871
(A)KG中蓝色实体的两层感受野(绿色实体)

KGCN层的最后一步是将实体表示 v 及其邻域表示$v^u_{s(v)}$ ==聚合成单个向量==。

我们在KGCN中实现了三种类型的聚合器agg：$\mathbb R ^d \times \mathbb R ^d \rightarrow \mathbb R ^d $ ：

  • Sum（求和）聚合器取两个表示向量之和，然后进行非线性变换
    image-20210402204501093
    其中W和b分别是变换权重和偏置，σ是像ReLU这样的非线性函数。
  • Concat（连接）聚合器[7]在应用非线性变换之前首先连接两个表示向量：
    image-20210402204622757
  • Neighbor（邻居）聚合器[15]直接将实体v的邻域表示作为输出表示：
    image-20210402204724792

聚合是KGCN中的关键步骤，因为==项目的表示通过聚合与其邻居绑定在一起==。我们将在实验中对这三个聚合器进行评估。

3.3 学习算法

通过==单个KGCN层==，实体的最终表示依赖于其自身及其直接邻居，我们将其命名为1阶实体表示。

将KGCN从一层扩展到多层，以更广、更深的方式合理挖掘用户的潜在兴趣，这是理所当然的。

该技术是直观的：将每个实体的初始表示(0阶表示)传播给它的邻居，得到1阶实体表示，然后我们可以重复这个过程，即进一步传播和聚合1阶表示，得到2阶表示。

一般而言，实体的h阶表示是其自身及其邻居的初始表示的混合，最远可达h跳。

这是KGCN的一个重要属性，我们将在下一小节中讨论。

上述步骤的形式描述在算法1中给出。

h表示接受场的最大深度(或者等效地，聚合迭代的次数)，由表示向量附加的后缀[h]表示h阶。

对于给定的用户-项目对(u，v)(第2行)，

我们首先以逐层迭代的方式计算感受野(第3行，13-19行)。

然后将聚合重复H次(第5行)：

在迭代h中，我们计算每个实体e∈M[h]的邻域表示(第7行)，

然后将其与其自己的表示EU[h−1]聚合，

以获得要在下一次迭代中使用的表示(第8行)。

最终的H阶实体表示被表示为vu(行9)，

它与用于预测概率的用户表示u一起被馈送到函数f：rd×rd→R中：

image-20210402210950370

image-20210402214108717

算法1：KGCN算法

  • 输入：
    • 交互矩阵Y；
    • 知识图谱G(E,R)；
    • 邻域抽样图S：$S:e \rightarrow 2^\xi $ ;
    • 可训练参数：${u}{u \in \mathcal U},{e}{e \in \mathcal E},{r}{r \in \mathcal R},{W_i,b_i}{i=1}^H $ ；
    • 超参数：H，d，g(·)，f(·)，σ(·)，agg(·)
  • 输出：
    • 预测函数 $\hat y _{uv} = \mathcal F(u,v | \Theta,Y,G) $

while (KGCN 不收敛时) do
for (u,v) in Y do
${M[i]}^H_{i=0} \leftarrow $ 获取感受野(v)；

​ $e^u[0] \leftarrow e , \forall e \in M[0]$

图1B示出了一次迭代中的KGCN算法，其中给定节点的实体表示Vu[h]和邻域表示(绿色节点)混合以形成其用于下一迭代(蓝色节点)的表示。

image-20210402211024736

(B)KGCN的框架

注意，算法1遍历所有可能的用户项对（第2行）。为了使计算更有效，我们在训练期间使用负面采样策略。完整的损失函数如下：

image-20210402214229685

其中$\mathcal L$是交叉熵损失函数(cross-entropy loss)，P是负的采样分布，$T^u$为用户u的负样本数。

在本文中，$T^u = |{v:y_{uv}=1}|$并且P遵循均匀分布。最后一个块是L2正则化矩阵。

4. 实验

4.1 数据集

我们在我们的电影，书籍和音乐推荐的实验中使用以下三个数据集：

  • MOVIELENS-20M：一个在电影推荐中广泛使用的基准数据集，其中MOVIELENS网站上的大约2000万只显式评级（从1到5）组成。
  • Book-Crossing：含有100万条书籍评级（从0到10），来自于Book-Crossing社区
  • Last.FM：包含来自Last.fm在线音乐系统的一组2,000个用户的听音乐信息。

由于三个数据集是显反馈，我们将它们==转换为隐反馈==，其中每个条目被标记为1表示用户积极评分，标记为0的表示用户消极评分。

对于Movielens-20m的积极评分的==阈值==为4，而由于其稀疏性没有为BookCrossing和Last.fm设置阈值。

我们使用Microsoft Satori来构建每个数据集的知识图谱。

我们首先从整个KG选择一个三元组，置信水平大于0.9。

给出Sub-KG，我们收集所有有效电影/书籍/音乐的的StaoriID，什么是有效呢，就是通过书籍/电影/音乐的名字与三元组的尾相匹配，比如(head，film.film.name,tail)，(head,book.book.title,tail)，(head,type.object.name,tail)。

具有多个匹配或没有匹配实体的项目被排除，因为其过于简单。

然后，我们将项目ID与所有三元组匹配，并从Sub-kg中选择所有匹配的三元组。

三个数据集的基本统计信息如表1所示。

表1：三个数据集的基本统计和超参数设置(K:邻居采样大小，d:嵌入维数，H:感受野深度，λ: L2正则化权重，η:学习率)。
image-20210407111819265

4.2 Baselines

我们将建议的KGCN与以下基线进行比较，其中前两个基线是无KG的，而其余的都是有KG使用的方法。基线的超参数设置将在下一小节中介绍。

  • SVD[11]：是一个经典的基于CF的模型，使用内积来建模用户-项目交互。（我们尝试过NCF [8]，即用神经网络代替内积，但结果不如SVD。由于SVD和NCF相似，我们在这里只呈现更好的一个。）
  • LibFM [14]：是CTR场景中基于特征的分解模型。我们连接 user ID 和 item ID 作为LibFM的输入。
  • LibFM + TransE：通过将TransE [1]学习的实体表示，附加到每个用户-项目对，来扩展LibFM
  • PER [22]：将KG视为异构信息网络，并提取基于元路径的特征，来表示用户和项目之间的连通性
  • CKE [23]将CF与结构、文本和视觉知识结合在一个统一的推荐框架中。在本文中，我们将CKE实现为CF加上一个结构知识模块。
  • RippleNet [18]是一种类似内存网络的方法，它将用户的偏好传播到KG上进行推荐。

4.3 实验设置

在KGCN，我们设置函数 g 和 f 为内积，σ在不是最后一层的时候用ReLU，在最后一层的时候用tanh。

表1提供了其他超参数设置。

超参数是通过在验证集上优化AUC（模型评估指标）来确定的。

对于每个数据集，训练集、评估集和测试集的比例为6 : 2 : 2。

每个实验重复3次，并报告平均性能。

我们在两个实验场景中评估了我们的方法:

(1)在点击率预测中，我们应用训练好的模型来预测测试集中的每个交互。我们使用UC和F1来评估CTR预测。

(2)在top-K推荐中，我们使用训练好的模型为测试集中的每个用户选择预测点击概率最高的K个项目，选择Recall@K对推荐集进行评价。

所有可训练参数均采用亚当算法优化。

Adam算法：

什么是Adam算法

Adam算法详解

KGCN-LS的代码是在Python 3.6、TensorFlow 1.12.0和NumPy 1.14.3下实现的

基线的超参数设置如下。

  • 对于SVD，我们使用无偏版本(即，预测评级被建模为$r_{pq}= p^⊤q$).

    • 四个数据集的维数和学习率分别设置为:
      • 对于MovieLens-20M和Book-Crossing，d = 8，η = 0.5；
      • 对于Last.FM，d = 8，η = 0.1；
      • 对于LibFM，维数为{1，1，8}，训练批次数epochs为50。TransE的维度是32。

  • 对于PER，我们使用手动设计的user-item-attribute-item路径作为特征

    • MovieLens-20M
      • “user-movie-director-movie”
      • “user-movie-genre-movie”
      • “user-movie-star-movie”
    • Book-Crossing
      • “user-book-author-book”
      • “user-book-genrebook”
    • Last.FM
    • “user-musician-date_of_birth-musician”(date of birth is 离散化的)
    • “user-musician-country-musician”,
    • “user-musician-genre-musician”

  • 对于CKE

    • 三个数据集的维数分别为64、128、64。
    • 对于所有数据集，KG部分的训练权重为0.1
    • 学习率和SVD一样。

  • 对于RippleNet

  • MovieLens-20M：d = 8，H = 2，λ1 = 106，λ2= 0.01，η= 0.01；

  • Last.FM：d = 16，H = 3，λ1 = 105，λ2= 0.02，η = 0.005。

  • 其他超参数与他们在原始论文中报告的相同，或在他们的代码中默认。

4.4 结果

对比结果

image-20210408170732277

CTR预测和top-K推荐的结果分别显示在表2和图2中(为了清楚起见，图2中没有绘制SVD、LibFM和KGCN的其他变量)。我们观察到以下情况:

  • 总的来说，我们发现KGCN在书籍和音乐方面的进步高于电影。这表明，KGCN可以很好地解决稀疏的场景，因为BookCrossing和Last.FM比MovieLens20M要稀疏得多。
  • 无KG基线(SVD和LibFM)的性能实际上优于两个KG感知基线(PER和CKE)，这表明PER和CKE不能充分利用具有手动设计的元路径和TransRlike正则化的KG。
  • LibFM + TransE在大多数情况下都比LibFM好，说明KG的引入总体上对推荐是有帮助的。
  • 在所有基线中，PER表现最差，因为很难在现实中定义最佳元路径。
  • 与其他基线相比，RippleNet显示出强大的性能。请注意，RippleNet还使用多跳邻域结构，有趣的是，这表明在KG中捕获邻近信息对于推荐至关重要。

image-20210408170704265

三种KGCN聚合器

表2中的最后四行总结了KGCN变体的性能。

前三个(和、串联、相邻)对应于前面部分介绍的不同聚合器，而最后一个变体KGCN-avg是KGCN-sum的简化情况，其中邻域表示被直接平均而没有用户关系分数(即vu N(v)=˝ e∈N(v)e而不是Eq)。(2)).

因此，KGCN-平均用于检验“注意机制”的功效。从结果中我们发现:

  • KGCN的表现明显优于所有基线，但它们的表现略有不同:==KGCN-sum总体表现最好==，而KGCNneighbor的表现在Book-Crossing和Last.FM上有明显差距。这可能是因为邻居聚合器仅使用邻域表示，因此从实体本身丢失了有用的信息。
  • KGCN-avg的表现比KGCN-sum差，尤其是在Bookcross和最Last.fm稀少的。这表明捕捉用户的个性化偏好和KG的语义信息确实有利于推荐。

邻居采样大小影响

image-20210408170836586
表3不同相邻样本大小KGCN曲线的AUC结果

4.4.1==邻居采样大小==的影响。我们通过改变样本邻居的大小来研究KG的使用效果。从表3中，我们观察到==当K = 4或8时，KGCN达到最佳性能==。这是因为太小的K没有足够的容量来合并邻域信息，而太大的K容易被噪声误导。

感受野深度影响

image-20210408170922909

4.4.2==感受野深度==的影响。我们研究了KGCN感受野深度的影响。结果如表4所示，==表明与k相比，KGCN对H更敏感。当H = 3或4时，我们观察到严重的模型崩溃的发生==，因为较大的H会给模型带来大量噪声。这也符合我们的直觉，因为当推断项目间相似性时，过长的关系链没有什么意义。根据实验结果，==1或2的H对于真实情况是足够的==。

嵌入维度影响

image-20210408171052321

4.4.3==嵌入维度==的影响。最后，我们检验了嵌入维度对KGCN绩效的影响。表5中的结果相当直观:==最初增加d可以提高性能==，因为较大的d可以编码更多的用户和实体信息，而==过大的d==会受到==过度拟合==的不利影响。

5. 总结展望

提出了一种用于推荐系统的知识图卷积网络。

KGCN将非谱GCN方法扩展到知识图，有选择地、有偏见地聚集邻域信息，不仅能学习知识图的结构信息和语义信息，还能学习用户的个性化和潜在兴趣。

我们还以小批量方式实现了所提出的方法，该方法能够在大数据集和知识图上操作。

通过在真实数据集上的大量实验，KGCN在电影、书籍和音乐推荐方面的表现一直优于最先进的基线。

我们指出了未来工作的三条途径。

  • (1)在这项工作中，我们从一个实体的邻居那里==统一取样==，以构建其感受野。探索==非均匀采样==(如重要性采样)是未来工作的一个重要方向。
  • (2)本文(和所有文献)集中于建模==item-end的KGs==。未来工作的一个有趣的方向是研究利用==user-edn的KGs==是否有助于提高推荐的性能。
  • (3)设计一种算法来很好地==结合两端的KGs==也是一个很有前途的方向。
文章作者: SongX64
文章链接: https://SongX64.github.io/2021/04/01/0401%E5%B0%86%E7%9F%A5%E8%AF%86%E5%9B%BE%E8%B0%B1%E5%8D%B7%E7%A7%AF%E7%BD%91%E7%BB%9C%E7%94%A8%E4%BA%8E%E6%8E%A8%E8%8D%90%E7%B3%BB%E7%BB%9F/
版权声明: 本博客所有文章除特別声明外，均采用 CC BY 4.0 许可协议。转载请注明来源 SongX64 !
科研 Knowledge Graph 论文翻译 Recommendation
赏
  目录