简单了解清华大学朱军珠算框架

珠算的基本概念

补充：张量

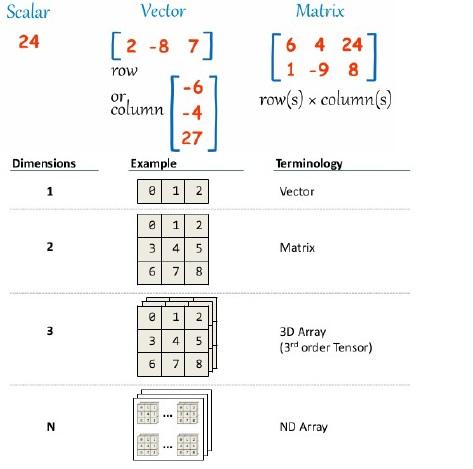
如图所示，0维就是数，1维是向量，2维是矩阵，3维以上就是张量了。当然一个1维向量也可叫做1维张量。

分布

分布

分布是构建概率模型的基本功能。 Distribution类是各种概率分布的基类，它支持批输入，生成批量样本并评估给定值批次的概率。

可用的分布：

单变量分布

多变量分布

我们可用珠算来创建一个单变量正态分布，代码如下：

>>> import zhusuan as zs
>>> a = zs.distributions.Normal(mean=0., logstd=0.)

分布典型的输入形状是像batch_shape + input_shape，其中batch_shape表示一个non-batch的输入参数的形状;batch_shape代表有多少个独立的输入变量被放到分布中。总的来说，分布支持boradcast的输入。

---

补充：boradcast机制

boradcast机制是numpy中的机制。TensorFlow中好像叫boradcasting机制……应该差不多吧。TensorFlow有不少操作支持boradcast。

举例如下：

>>> import numpy as np
>>> a = np.arange(0, 6).reshape(6, 1)
>>> a
array([[ 0], [1], [2], [3], [4], [5]])
>>> a.shape
(6, 1)
>>> b = np.arange(0, 5)
>>> b.shape
(5,)
>>> c = a + b
>>> print c
[[0 1 2 3 4]
 [1 2 3 4 5]
 [2 3 4 5 6]
 [3 4 5 6 7]
 [4 5 6 7 8]
 [5 6 7 8 9]]

图解：

不同维度向量相加，可以自动填充。

官方示例图：

更全的一个图：（矩阵+矩阵，矩阵+向量，向量+向量）

广播机制的规则：

1. 让所有输入数组都向其中shape最长的数组看齐，shape中不足的部分都通过在前面加1补齐

   （这是是说shape+1,矩阵中数据是复制的)

2. 输出数组的shape是输入数组shape的各个轴上的最大值

   （例如上面的5和6）

3. 如果输入数组的某个轴和输出数组的对应轴的长度相同或者其长度为1时，这个数组能够用来计算，否则出错

   （如果有多行的话就不知道复制哪一行了，所以说要求是1）

4. 当输入数组的某个轴的长度为1时，沿着此轴运算时都用此轴上的第一组值

   （复制第一行）

TensorFlow, numpy中的broadcast机制

---

可以通过调用distribution对象的sample()方法来创建例子。它的形状是([n_samples] + )batch_shape + value_shape。只有当传递的n_samples为None(默认情况下)时，才会省略第一个附加轴.，在这种情况下创建一个样本。value_shape是非批次输入值的分布的形状。对于一个单变量分布来说，它的value_shape是[]。

---

补充：axis参数

axis是许多函数中都有的一个参数，直接翻译是轴。其实是对于张量来说的一个概念。如下：

#python
x=[[1,2],[5,1]]
x=np.array(x)
z1=np.max(x,axis=0)
z2=np.max(x,axis=1)


#tensorflow
x=tf.constant([[1.,2.],[5.,2.]])  
x=tf.shape(x)  
z1=tf.reduce_max(x,axis=0)#沿axis=0操作  
z2=tf.reduce_max(x,axis=1)#沿axis=1操作

​ 类似的还有argmax，sum等等函数，它们都含有一个名为axis的参数，那这个参数到底是什么意思呢？一句话总结就是：沿着axis指定的轴进行相应的函数操作。

​ 对于2维来说，axis=0就是列，axis就是行，这里不再详解。直接理解3维的。

>>> z
array([[[ 2,  3,  4,  8],
        [ 3,  1,  4,  1],
        [ 6,  3,  2,  6]],

       [[10,  2, 45,  2],
        [ 2,  4,  5, 10],
        [22,  4,  4,  1]]])
>>> z.shape
(2, 3, 4)

​ 这是一个2x3x4的3维张量，或者直接说是三维数组。

​ 接下来我们看一下max()为例，取不同axis的形状：

>>> np.max(z,axis=0).shape
(3, 4)
>>> np.max(z,axis=1).shape
(2, 4)
>>> np.max(z,axis=2).shape
(2, 3)

​ 也就是说，axis取几，就去掉那个维度。这里的axis是对应shape中的第几个数，也就是第几维。比如axis=0就是说(2,3,4)中的2; axis=1就是对应3……以此类推。

​ 其计算的最后输出结果如下：

>>> np.max(z,axis=0)
array([[10,  3, 45,  8],
       [ 3,  4,  5, 10],
       [22,  4,  4,  6]])
>>> np.max(z,axis=1)
array([[ 6,  3,  4,  8],
       [22,  4, 45, 10]])
>>> np.max(z,axis=2)
array([[ 8,  4,  6],
       [45, 10, 22]])

​ 解释一下，比如axis=0，那么它的输出就是去掉第一维度的影响，也就是(2,3,4)中去掉2，应该是个(3,4)的张量，如上所示。也就是说，去掉0这个轴，也就是说去掉开始的这个2维的影响。那么我们可以看做是z[]中的2个元素相互重叠，降维。

​ 再比如说axis=1，那么就是去掉3的影响，得到结果应该是个(2,4)的张量。也就是对于z[0]和 z[1]分别考虑，取出一个（4）的张量。同时也就是说去掉3行的影响，也就是说按列来对比。

​ 对于三维张量来说，如图所示：

​ 理解为降维即可，就是把那个轴上的数压缩一下到一个平面上。2是axis=0；3是axis=1；4是axis=2。

​ 四维及其更高虽然说不能展示出来，但是可以通过相同的方式来理解。也就是看得到的结果是几维的，然后相应的比较。其他sum函数等等同理，只是对于数的操作不同，这里是取max，sum就是把重叠的数加起来啦。

---

单变量/多变量分布实例

• 单变量分布(正态分布)的例子：

>In[3]:
import zhusuan as zs
import tensorflow as tf
_ = tf.InteractiveSession()
b = zs.distributions.Normal(
 [
     [[-1.,1.],[-1.,-2.]],
        [[9.,1.],[1.,2.]]
    ],logstd=[0.,1.])
   
   
In [4]:# batch_shape显示有多少批被输入到分布的形状中
# 这里是2维有2个，1维有2个，0维有2个
# 或者这样说：[2,2,2]三个数表示有3层，第一层里面有2，第二层里面有2，第三层里面有2
b.batch_shape.eval()

Out[4]:array([2, 2, 2])


In [5]:b.value_shape.eval()
 
Out[5]:array([], dtype=int32)
   

In [9]:tf.shape(b.sample()).eval( )

Out[9]:array([2, 2, 2])

 
In [11]:tf.shape(b.sample(1)).eval()
   
Out[11]:array([1, 2, 2, 2])

 
In [12]:tf.shape(b.sample(2)).eval()
   
Out[12]:array([2, 2, 2, 2])

 
In [13]:b.get_batch_shape()
   
Out[13]:TensorShape([Dimension(2), Dimension(2), Dimension(2)])

 
In [14]:b.get_value_shape()
   
Out[14]:TensorShape([])

多变量分布的例子（使用oneHot分类）：

>import zhusuan as zs
import tensorflow as tf
_ = tf.InteractiveSession()

c = zs.distributions.OnehotCategorical([[0.,1.,-1.],
                                     [2.,3.,4.]])
# batch，批次，2个批次，也就是说是2维数组
   c.batch_shape.eval()
array([2])

# 每个批次有3个数
c.value_shape.eval()
array([3])

tf.shape(c.sample()).eval()
array([2, 3])

tf.shape(c.sample(1)).eval()
array([1, 2, 3])

tf.shape(c.sample(10)).eval()
array([10,  2,  3])

# 输出一下这两个shape看看
print('c.batch_shape == ',c.batch_shape)
print('c.batch_shape.eval() == ',c.batch_shape.eval())
print('c.value_shape == ',c.value_shape)
print('c.value_shape.eval() == ',c.value_shape.eval())

c.batch_shape ==  Tensor("shape_as_tensor_13:0", shape=(1,), dtype=int32)
c.batch_shape.eval() ==  [2]
c.value_shape ==  Tensor("shape_as_tensor_15:0", shape=(1,), dtype=int32)
c.value_shape.eval() ==  [3]

# 输出一下sample
print('c.sample() == ',c.sample().eval())
print('c.sample(1) == ',c.sample(1).eval())
print('c.sample(10) == ',c.sample(10).eval())

c.sample() ==  [[0 1 0]
[0 0 1]]
c.sample(1) ==  [[[0 1 0]
 [1 0 0]]]
c.sample(10) ==  [[[0 1 0]
  [0 0 1]]

  [[0 1 0]
[0 0 1]]
 
  [[0 0 1]
[0 0 1]]
 
  [[0 1 0]
[0 0 1]]
 
  [[0 1 0]
[0 1 0]]
 
  [[0 1 0]
[0 1 0]]
 
  [[0 1 0]
[0 0 1]]
 
  [[0 1 0]
[0 0 1]]
 
  [[1 0 0]
[0 0 1]]
 
  [[0 1 0]
[0 0 1]]]

在某些情况下，一批随机变量可以分组到一个独立事件中，以便于可以一起计算他们的概率。这是通过设置group_ndims参数（默认是0）来实现的。batch_shape中最后的group_ndims个批次被分组为一个事件。 例如，Normal(…，group_ndims = 1）会将其batch_shape的最后一个axis设置为独立事件，即具有一致协方差矩阵（在统计学与概率论中，协方差矩阵的每个元素是各个向量元素之间的协方差，是从标量随机变量到高维度随机向量的自然推广）的多元正态分布。

---

补充：_ = tf.InteractiveSession()

TensorFlow的前后端的连接依靠于session，使用TensorFlow程序的流程构建计算图完成之后，在session中启动运行。

补充：Sesssion

我们在Python中需要做一些计算操作时一般会使用NumPy，NumPy在做矩阵操作等复杂的计算的时候会使用其他语言(C/C++)来实现这些计算逻辑，来保证计算的高效性。但是频繁的在多个编程语言间切换也会有一定的耗时，如果只是单机操作这些耗时可能会忽略不计，但是如果在分布式并行计算中，计算操作可能分布在不同的CPU、GPU甚至不同的机器中，这些耗时可能会比较严重。
TensorFlow 底层是使用C++实现，这样可以保证计算效率，并使用 tf.Session类来连接客户端程序与C++运行时。上层的Python、Java等代码用来设计、定义模型，构建的Graph，最后通过tf.Session.run()方法传递给底层执行。

对于像Python原生编辑器，或者jupyter这样的基于浏览器的python编辑器，要一段一段的输入代码， 于是就有了 tf.InteractiveSession() 这样的交互式会话，它不需要用 “sess.run(变量)”这种形式，而是定义好会话对象后，每次执行tensor时，调用tensor.eval()即可。

补充：eval()

eval() 其实就是tf.Tensor的Session.run() 的另外一种写法，但两者有差别:

1. eval(): 将字符串string对象转化为有效的表达式参与求值运算返回计算结果
2. eval()也是启动计算的一种方式。基于Tensorflow的基本原理，首先需要定义图，然后计算图，其中计算图的函数常见的有run()函数，如sess.run()。同样eval()也是此类函数，
3. 要注意的是，eval()只能用于tf.Tensor类对象，也就是有输出的Operation。对于没有输出的Operation, 可以用.run()或者Session.run()；Session.run()没有这个限制。

贝叶斯网络

在ZhuSuan中，我们支持将概率模型构建为贝叶斯网络，即定向图形模型。 下面我们使用一个简单的贝叶斯线性回归示例来说明这一点。 模型的生成过程是
$$
w \mbox{} N(0,\alpha^2I)\
y \mbox{} N(w^Tx,\beta^2)
$$
其中x表示线性回归中的输入特征。 我们应用贝叶斯处理并假设回归权重w的正态先验分布。 假设输入要素有5个维度。 为简单起见，我们将输入定义为占位符并设置超参数：

x = tf.placeholder(tf.float32, shape=[5])
alpha = 1.
beta = 0.1

---

补充：超参数 hyper-parameters

1. 参数(parameters)/模型参数

　由模型通过学习得到的变量，比如权重w和偏置b

2. 超参数(hyperparameters)/算法参数

   根据经验进行手动设定，影响到权重w和偏置b的大小，比如迭代次数、隐藏层的层数、每层神经元的个数、学习速率等

补充：tf.placeholder()

定义‘符号’变量，也称为占位符。相当于定义一个变量，但是不赋值，到了使用的时候再进行赋值。

​ Tensorflow的设计理念称之为计算流图，在编写程序时，首先构筑整个系统的graph，代码并不会直接生效，这一点和python的其他数值计算库（如Numpy等）不同，graph为静态的，类似于docker中的镜像。然后，在实际的运行时，启动一个session，程序才会真正的运行。这样做的好处就是：避免反复地切换底层程序实际运行的上下文，tensorflow帮你优化整个系统的代码。我们知道，很多python程序的底层为C语言或者其他语言，执行一行脚本，就要切换一次，是有成本的，tensorflow通过计算流图的方式，帮你优化整个session需要执行的代码，还是很有优势的。

​ 所以placeholder()函数是在神经网络构建graph的时候在模型中的占位，此时并没有把要输入的数据传入模型，它只会分配必要的内存。等建立session，在会话中，运行模型的时候通过feed_dict()函数向占位符喂入数据。

---

BayesianNet实例

要定义模型，第一步是构造一个BayesianNet实例：

bn = zs.BayesianNet()

贝叶斯网络将一组随机变量的联合分布的依存关系描述为有向图。 为此，BayesianNet实例可以保留两种节点：

• 随机节点。 它们是图形模型中的随机变量。 w节点可以构造为：

w = bn.normal("w", tf.zeros([x.shape[-1]]), std=alpha)

这里w是一个服从正态分布的StochasticTensor随机张量（StochasticTensor类，类似于Tensor，可以被传到任何Tensor操作中）:

>>> print(w)
<zhusuan.framework.bn.StochasticTensor object at ...

对于zhusuan.distributions中任何可用的分布，我们都能在BayesianNet中找到一个方法来创建相应的随机节点。StochasticTenor实例类类似于Tensor，这意味着你可以将StochasticTenor类与任何TensorFlow原语混用。例如，线性回归的预测均值是w与输入x之间的内积：

y_mean = tf.reduce_sum(w * x, axis=-1)

StochasticTenor类说明

插一句，这里的axis=-1就是说倒数第一个。比如（3,4,5）,axis=-1就是指5，也就是等价于axis=2。

w节点的构造，=bn.nomal(“节点名”，tf构造的全为0的一个数组【维度为x.shape】，标准差为上面定义的alpha)

这里还是关于-1的写法，x.shape[-1]就相当于x.shape[5].

print(w.shape,x.shape)
(5,) (5,)

补充：tf.reduce_sum()

reduce_sum应该理解为按相应的轴压缩求和，用于降维。通过设置axis参数按相应轴压缩求和。

关于上面那个内积的计算举例：

a=tf.constant([1,2,3,4,5])
b=tf.constant([2,2,2,2,2])
c = a*b
c.eval()

Out:array([ 2,  4,  6,  8, 10])

tf.reduce_sum(a*b,axis=-1).eval()

Out:30

---

确定性节点

• 确定性节点。

确定性节点。 如上面的代码所示，可以使用Tensorflow操作直接构造确定性节点，而BayesianNet不会跟踪它们。 但是，在某些情况下，可以通过deterministic（）方法启用跟踪：

y_mean = bn.deterministic("y_mean", tf.reduce_sum(w * x, axis=-1))

这使你可以随时从bn获取y_mean张量。

也就是说，如果在构建过程中这样写的话：

y_mean = tf.reduce_sum(w * x, axis=-1)

​ 那么bn中将不会有y_mean这个节点的信息。

# 康康这个模型里面有啥节点
print(model_b.nodes.keys())

Out: dict_keys(['w', 'y_mean', 'y'])

​ 换成deterministic()方法的话，那么就可以从bn中get到y_mean了。

# 康康这个模型里面有啥节点
print(model_b.nodes.keys())

Out: dict_keys(['w', 'y_mean', 'y'])

构建贝叶斯网络的完整代码

构建贝叶斯线性回归模型的完整代码如下：

def bayesian_linear_regression(x, alpha, beta):
 	bn = zs.BayesianNet()
 	w = bn.normal("w", mean=0., std=alpha)
 	y_mean = tf.reduce_sum(w * x, axis=-1)
 	bn.normal("y", y_mean, std=beta)
 	return bn

步骤总结：

1. 声明贝叶斯网络实例；

2. 构建一个随机节点w，使用正态分布，均值为0，标准差为alpha。w节点如下公式。

$$
w \mbox{~} N(0,\alpha^2I)
$$

3. 求w*x的和，也就是内积

4. 构建一个名为y的随机节点，使用正态分布，均值为w与x的内积，标准差为beta。x是占位符，传递过来的一个参数，应该是后来要输入的数据。y节点如下公式。
   $$
   y \mbox{~} N(w^Tx,\beta^2)
   $$

图形模型的一个独特的特点是允许随机节点具有不确定的行为（即是潜在的），我们可以随时观察它们（然后将它们固定在观察值上）。 在ZhuSuan中，可以使用观察到的字典参数来初始化BayesianNet，以将观察值分配给某些随机节点，例如：

bn = zs.BayesianNet(observed={"w": w_obs})

会使得随机变量w 作为w_obs被观察。这样做的的结果是在bn中，y_mean是根据w的观测值（w_obs）计算的。 对于未被观察的随机节点，当相应的StochasticTensor参与使用Tensor的计算或feed到Tensorflow操作中时，将使用其sample。 在此示例中，这意味着如果我们不对bn进行任何观察，则w的sample将会被用于计算y_mean。

尽管上述方法允许将观察值分配给随机节点，但在大多数情况下，首先定义图形模型然后在需要时传递观察值更为方便。 此外，该模型应允许查询具有不同观察值配置。 为了启用此工作流程，我们引入了一个新的类MetaBayesianNet。 从概念上讲，我们可以将MetaBayesianNet实例视为原始模型，并将BayesianNet视为确定的观察结果。 正如我们将看到的那样，BayesianNet实例可以从其元类实例惰性构造。

我们要将模型定义为MetaBayesianNet是非常容易办到的。 上面的代码没有任何变化，只是向该函数添加了一个函数装饰器：

@zs.meta_bayesian_net(scope="model")
def bayesian_linear_regression(x, alpha, beta):
 bn = zs.BayesianNet()
 w = bn.normal("w", mean=0., std=alpha)
 y_mean = tf.reduce_sum(w * x, axis=-1)
 bn.normal("y", y_mean, std=beta)
 return bn

由zs.meta_bayesian_net()注释的函数将返回MetaBayesianNet而不是原始的BayesianNet实例：

>>> model = bayesian_linear_regression(x, alpha, beta)

>>> print(model)
<zhusuan.framework.meta_bn.MetaBayesianNet object at ...

正如我们已经提到的，MetaBayesianNet可以允许不同的观察配置。 这是通过其observe()方法实现的。 我们可以将观察值作为命名参数传递，它将返回相应的BayesianNet实例，例如：

bn = model.observe(w=w_obs)

会将w在BayesianNet类返回的实例bn中设置为被观察的。 使用不同的命名参数调用上述函数（observe)，可以用不同的观察结果observation实例化BayesianNet，这类似于概率图模型的常见行为。

传递的观测值observation必须与StochasticTensor具有相同的类型和形状。

如果你在模型构造函数中创建了TensorFlow变量，你可能想将其重用于具有不同观察值的贝叶斯网络实例。 ZhuSuan中还有另一个函数装饰器，称为reuse_variables（），以方便使用。你可以将其添加到任何创建Tensorflow变量的函数中：

# 构建BayesianNet重用变量
@zs.reuse_variables(scope="model")
def build_model(...):
 bn = zs.BayesianNet()
 ...
 return bn

或等效地，在@zs.meta_bayesian_net（）装饰器中打开redirect_variables选项：

# 构建MetaBayesianNet重用变量
@zs.meta_bayesian_net(scope="model", reuse_variables=True)
def build_model(...):
 bn = zs.BayesianNet()
 ...
 return bn

总结：MetaBayesianNet与BayesianNet

MetaBayesianNet类是可变的BayesianNet，可以通过传递不同的观察值来构建贝叶斯网络。

在一个构造BayesianNet的函数上加个装饰器就将返回值转变为MetaBayesianNet。

这里的那个observed或许应该是:

bn = zs.BayesianNet(observed={"w_obs": w})

不然写{“w”:w_obs}的话会找不到w_obs报错。

自我否定：这里人家写的没错！

​ 这里的w_obs应该是个自定义的张量，通过把它传递过来对贝叶斯net进行不同的训练。也就是说可以吧贝叶斯网络中的w节点也作为一个参数。

​ 应该先自定义一个w_obs传过来。

到目前为止，我们知道如何构建模型并将其重用于不同的观察结果。 构建完成后，BayesianNet支持查询网络当前状态，例如：

># get named node(s)    获取节点名称
>w = bn["w"]
>w, y = bn.get(["w", "y"])

># get log probabilities of stochastic nodes conditioned on the current
># value of other StochasticTensors.
># 以其他Stochastic Tensor的当前值为条件获取随机节点的log对数概率
>log_pw, log_py = bn.cond_log_prob(["w", "y"])

># get log joint probability given the current values of all stochastic
># nodes
># 给定所有随机节点的当前值，获得对数联合概率
>log_joint_value = bn.log_joint()

默认情况下，对数联合概率是通过对所有随机节点上的条件对数概率求和而得出的。 这就要求所有随机节点的分配批处理形状正确对齐。 如果不是，则返回值可以是任意的。 大多数时候，您可以调整随机节点的group_ndims参数来解决此问题。 如果不是这种情况，我们仍然可以通过在MetaBayesianNet实例中重写它来自定义对数联合概率函数，如下所示：

>meta_bn = build_linear_regression(x, alpha, beta)

>def customized_log_joint(bn):
   return tf.reduce_sum(
       bn.cond_log_prob("w"), axis=-1) + bn.cond_log_prob("y")

>meta_bn.log_joint = customized_log_joint

然后，由这个meta_bn构建的所有BayesianNet实例将使用所提供的自定义函数来计算bn.log_joint()的结果。

cond_log_prob()函数

cond_log_prob(name_or_names)

The conditional log probabilities of stochastic nodes, evaluated at their current values (given by StochasticTensor.tensor).

随机节点的条件对数概率，按其当前值计算( 由StochasticTensor.tensor给出 )。

Parameters:	name_or_names – A string or a list of strings. Name(s) of the stochastic nodes.

Returns:	A Tensor or a list of Tensors.

log_joint()函数

log_joint()

The default log joint probability of this BayesianNet. It works by summing over all the conditional log probabilities of stochastic nodes evaluated at their current values (samples or observations).

该贝叶斯网络的默认对数联合概率。 它以随机节点当前值（sample或者是observations)的所有条件对数概率相加的方式来得到最终结果。

Returns: A Tensor.

补充：字典

​ 字典是另一种可变容器模型，且可存储任意类型对象。

​ 字典的每个键值 key=>value 对用冒号 : 分割，每个键值对之间用逗号 , 分割，整个字典包括在花括号 {} 中 ,格式如下所示：

d = {key1 : value1, key2 : value2 }

​ 值可以取任何数据类型，但键必须是不可变的，如字符串，数字或元组。

​ 一个简单的字典实例：

dict = {'Alice': '2341', 'Beth': '9102', 'Cecil': '3258'}

​ 也可如此创建字典：

dict1 = { 'abc': 456 } 
dict2 = { 'abc': 123, 98.6: 37 }

• 参考：菜鸟教程：字典

补充：函数装饰器

Python中的函数装饰器，写法注解一样。。。 所谓的装饰器，就是通过装饰器函数，来修改原函数的一些功能，使得原函数不需要修改。

详细见：Python@函数装饰器及其用法

补充：惰性函数

惰性函数好像是js中的一个概念？

具体讲解：JS高阶-惰性函数

JS惰性函数，是针对优化频繁使用的函数。常用于函数库的编写、单例模式之中。

惰性载入表示函数执行的分支只会在函数第一次掉用的时候执行，在第一次调用过程中，该函数会被覆盖为另一个按照合适方式执行的函数，这样任何对原函数的调用就不用再经过执行的分支了。

补充：贝叶斯线性回归

x为自变量，输入值； y为输出值。

1. 频率派线性回归：y = ax + b（一元）

​ y=β^T X+ω （多元，其中的各项均为向量）

2. 贝叶斯线性回归：y ~ N(w^t x,β^2)

​ 其中的各项变量应该为分布